• Education
• University Works
• Independent Works
• Music

• Independent Works
  • Analysis of Discrete Geometrical Structures
  • Monte Carlo Algorithm for Stage Climbing Problem

Sociality Function

In the case of points arranged in a line, the algorithm is simply that each point joins with the point clearly lying closest to it, which means no other point is allowed to have the same distance. Although the algorithm is simple and can be programmed to get the resulting number of emerging point groups and their sizes, the function lying behind it does not seem to be trivial. Depending on the number of points, a different number of groups and groups of different sizes are created that vary a lot and are not monotonically increasing or decreasing.

Counts of Group Sizes per Index

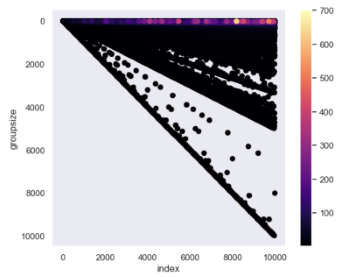
This heatmap shows the number of group sizes that are created per index. You can see that for smaller group sizes there are up to hundreds of groups with identical size. Another interesting observation in this vizualisation is that lines are created, which shows a correlation between the indices. The line dividing the picture in the middle consists of the samples where the groupsize is equal to the index, meaning only one group is created.

Number of Groups

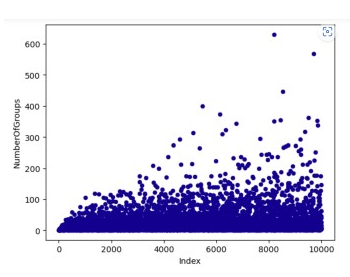
This scatter plot maps the index to the number of groups that are created. The number of emerging groups stays rather constantly in the range from 1 to 100, even though with higher indices the number of higher valued "outliers" increases.

Close Up Number of Groups

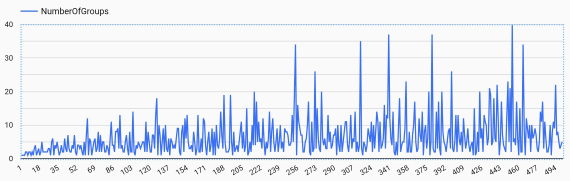
This line chart is a close up to the number of emerging groups from indices 0 - 500.